量子コンピューターを理解するための 量子力学入門
第1回 量子コンピューターを巡る誤解-なぜ「計算が速い」と言えるのか?
誤解②:量子コンピューターは非常に多くの計算を同時に行うことができる
並列計算の結果は一つだけ──量子ビット観測の落とし穴
そもそも量子コンピューターが従来のコンピューターと比べて、計算回数を劇的に減らせる可能性があるのは、量子力学に基づいた「重ね合わせ状態」を巧みに利用するからだ。
従来のコンピューターは、0または1の値を取る「ビット」を情報の最小単位としている。電流を流す状態と流さない状態を1と0で表すといった具合だ。一方で、量子コンピューターが扱う情報の最小単位は「量子ビット(qubit)」と呼ばれる。量子ビットは、重ね合わせ状態を実現することで、0と1を同時に表現することができる(図1)。
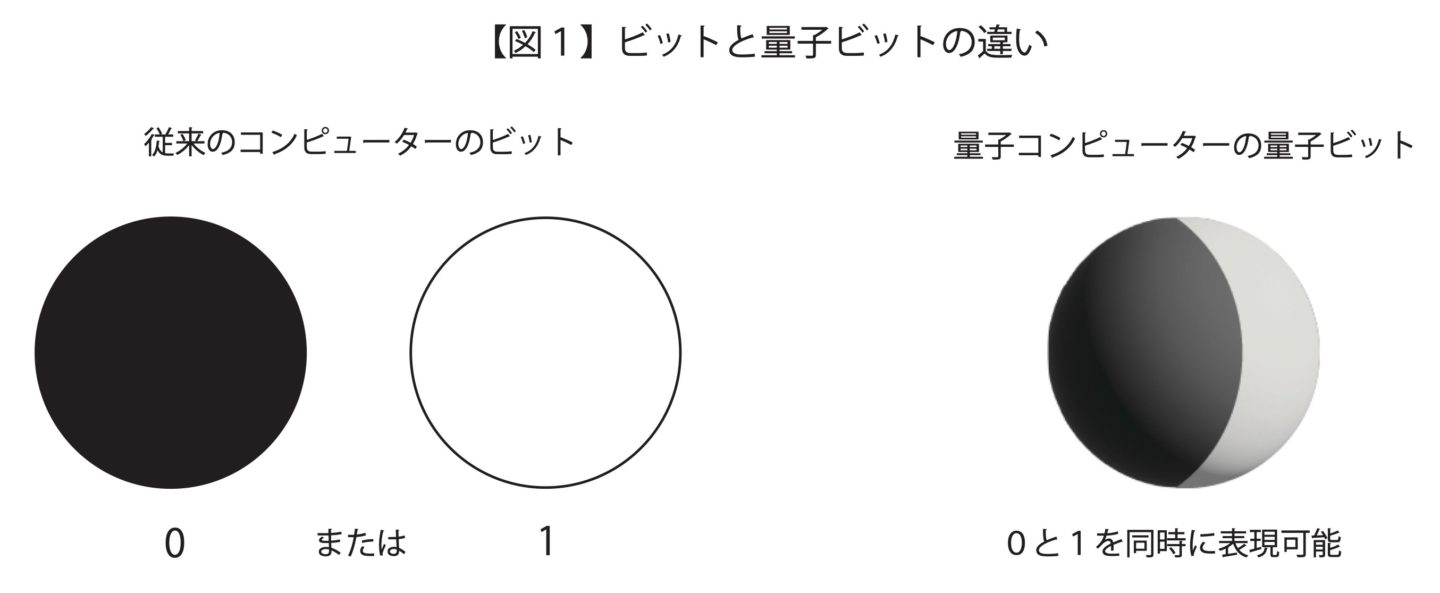
図1:ビットと量子ビットの違い
たとえば、従来のコンピューターで2ビットを使い、00、01、10、11(十進法の数で言うと0、1、2、3に対応)という4つの数値を入力して計算を行う場合、それぞれを別々に入力する必要があるので4回の計算が必要になる。
一方、量子コンピューターの場合、2つの量子ビットを使ってこれら4つの数値を同時に表現できる。つまり入力が1回で済んでしまうのだ。3個の量子ビットがあれば、従来のコンピューターの3ビットで8回の入力(2×2×2通りの数値の入力)が必要なところを1回の入力で済み、50個の量子ビットがあれば、従来のコンピューターで約1000兆回(2の50乗)の入力が必要なところを1回の入力で済む。n個の量子ビットがあれば、従来のコンピューターで2n回の入力が必要なところを1回の入力で済むわけだ。つまり、量子コンピューターは、原理的には量子ビットの個数が増えるにつれて、その計算性能が指数関数的に向上していくのである。
以上のことから、量子コンピューターは、非常に多くの計算を同時に行うことができる、と説明されることが多いのだが、これは半分は合っているが、大事なところを見落としている。たとえば、2量子ビットの計算で4つの計算を同時に行う場合、計算結果を得るためには、計算後の量子ビットを「観測」する必要がある。それぞれの量子ビットが0なのか1なのかを、観測によって知る必要があるわけだ。
しかし量子ビットは観測すると、重ね合わせ状態が崩れてしまうという性質がある。観測した瞬間、量子ビットは0か1かのどちらかの状態に確定してしまうのだ(図2)。
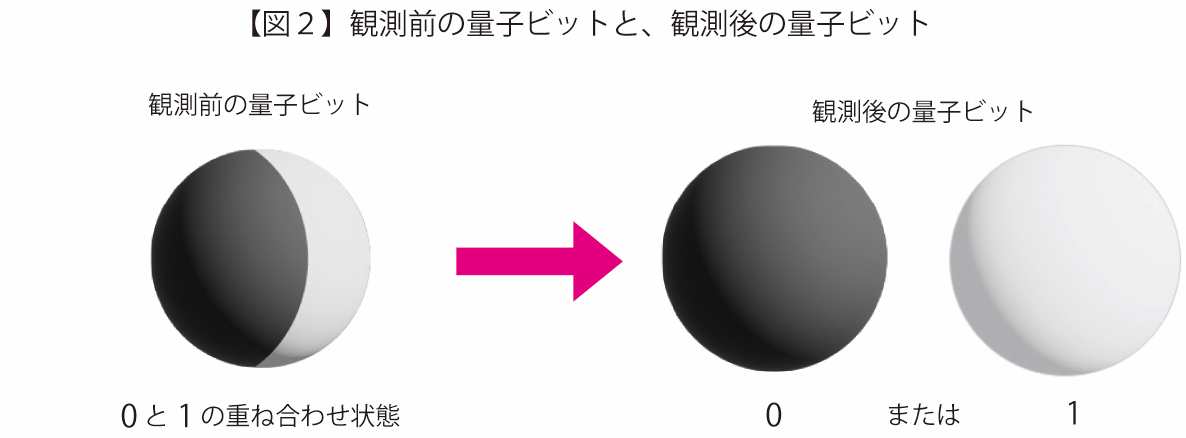
図2:観測前の量子ビットと、観測後の量子ビット
例えば、2量子ビットの場合、00、01、10、11の入力に対応する4つの計算結果がすべて得られるわけではない。4つの計算結果の重ね合わせ状態は観測によって崩れ、1つの計算結果だけしか得られないのだ。しかもどの計算結果が得られるかはランダム(確率的に)に決まる。量子コンピューターも従来のコンピューターと同じく、1回の入力で得られる計算結果は1つだけなのだ。
なお、重ね合わせ状態の観測については、連載の別の回で掘り下げて解説する予定である。
意味ある結果を引き出すには「量子アルゴリズム」が必須
量子コンピューターで意味のある計算を行うには、問題ごとに、欲しい計算結果が観測される確率が圧倒的に高くなるような計算の工夫が必要となる(干渉とよばれる現象を利用する)。このような問題ごとに設計される、量子力学に基づいた特殊な計算の手順は「量子アルゴリズム」と呼ばれている。
古くから知られている有名な量子アルゴリズムには、高速に素因数分解を行う「ショアのアルゴリズム」がある。たとえば、24の素因数分解を行うことを考えよう。単純なやり方は、24を手当たり次第の素数で割っていき、余りが出るかを調べていく、というものだ。実際にやってみると、24=2×2×2×3=23×3になる。この程度の小さい数の素因数分解なら、従来のコンピューターでも可能だが、整数の桁が大きくなってくると、素因数分解をするための計算回数は爆発的に増加してしまい、手に負えなくなってしまう。一方、ショアのアルゴリズムでは、量子ビットの重ね合わせ状態を利用して、素因数分解の一部の計算を行う。このとき、正しい答えの観測確率だけが高くなるように計算手順が工夫されているのだ。
実はこの「素因数分解の難しさ」は、インターネット通信の「RSA暗号」の安全性の根拠となっている。盗聴者が暗号化された情報を元に戻す(復号する)には、巨大な数の素因数分解を行う必要がある。従来のコンピューターでは巨大な数を素因数分解することが(現実的な時間内には)できないという事実によって、RSA暗号の安全性は保たれているのだ。
しかし、量子コンピューターが実用化すれば、ショアのアルゴリズムを使ってRSA暗号を破ることが可能になり、通信の安全性が確保できなくなってしまうとされる。ただし現在のRSA暗号を破るには、数百万〜数億個の量子ビットが必要と言われている。現状で実現しているのは数十〜数百量子ビット程度なので、近い将来にRSA暗号が破られる心配をする必要は、今のところなさそうだ。
他に知られている量子アルゴリズムには、たくさんのデータの中から望みのデータを探し出す「グローバーのアルゴリズム」などがある。現在知られている量子アルゴリズムは60ほどある。逆にいえば、実用化レベルの量子コンピューターが完成したとしても、現時点ではこれら以外の計算の用途には使えないことになる。
量子ビットが具体的にどのようなものなのかは、連載の次回以降で詳しく解説する予定だ。
関連記事
-
 FEATURE2025.03.31
FEATURE2025.03.31AIが拡げる生命科学の可能性─藤田医科大学教授・八代嘉美氏に聞く
第1回 AI開発者がノーベル化学賞を受賞した意味2025.03.31聞き手 都築 正明 -
 REVIEW2022.12.05
REVIEW2022.12.05“神の手”から“AIの眼”へ──審判の消失と人間存在の再定義
ワールドカップが求めた数学的な正しさと、ポストヒューマニズムの行方2022.12.05テキスト 桐原 永叔 -
 FEATURE2023.12.13
FEATURE2023.12.13ジャーナリスト・服部桂氏に聞く
(3)地球全体を外側から眺めるという知的な革命2023.12.13聞き手 都築正明(IT批評編集部)
桐原永叔(IT批評編集長)





