量子コンピューターを理解するための 量子力学入門
第3回 量子力学で書き換えられた「実在」の概念
──「1つの電子は複数の場所に同時に存在できる」そう考えざるを得ない驚きの実験

連載の第1回、第2回では、量子コンピューターの仕組みを理解するには「重ね合わせ状態」について理解する必要がある、ということを何度も述べてきた。重ね合わせ状態とは、例えば、「1つの電子が複数の場所に同時に存在している状態」のことである。常識的な感覚からすれば、そんなことはありえないはずで、「納得できない」と思われた方も多いことだろう。そこで今回は、重ね合わせ状態を認めないと説明できない「2重スリット実験」という有名な実験を紹介しよう。2重スリット実験を通して、重ね合わせ状態と密接な関係がある「電子の波」が何なのかについても詳しく解説していく。
執筆者プロフィール
科学ライター・編集者。大学では応用物理学を専攻。20年以上にわたり、科学全般について取材してきた。特に興味のある分野は物理学、宇宙、生命の起源、意識など。
目次
「電子の波」と重ね合わせ状態の関係
─電子の波とは何か?
─ミクロな粒子は”モノ”でもあり、”コト”でもある!?
2重スリット実験
─光は2重スリット実験によって、「波」であることが実証された
─「世界一美しい実験」と称された電子の2重スリット実験
─スリットの先では、2つの波が「重ね合わせ状態」になっている
─どちらのスリットを通過したかを確認すると、干渉縞は現れない
「波と粒子の2重性」とは結局、何なのか?
─電子は粒子でもなければ、波でもない
─量子力学を難しいと感じるのは、私たちの思考が”実数的”だからかもしれない
「電子の波」と重ね合わせ状態の関係
電子の波とは何か?
実は連載の第1回、第2回であえて説明を省いてきた量子力学の重要な概念がある。それは「電子のようなミクロな粒子は、波のような性質をもつ」ということだ。これは「波と粒子の2重性」などと呼ばれる。
一番わかりやすい波の例は、水面の波だ。水面に葉っぱを浮かべ、そこを波が通過すると、葉っぱは上下に「振動」する[1]。このことからも分かるように、水面の波とは「水の振動が広がっていく現象」だと言える。身近な波には他にも音波、地震波などがある。音波は空気の振動、地震波は地面や岩盤などの振動である[2]。つまり身近な波は、何らかのモノの振動が広がっていく現象(コト)だと言えるわけだ。
[1]正確に言うと、水面の波は、水の各部分が上下ではなく、楕円もしくは円を描くように振動している。
[2]身近な波には、他にも電磁波がある。電磁波は波長(波の山の頂点から隣の山の頂点までの長さ)の長い方から、電波、赤外線、可視光線(いわゆる光)、紫外線、X線、ガンマ線に分けられる。電磁波は物質の振動ではなく、電場と磁場の振動である。
一方、電子の波は、何かのモノの振動が広がっていく現象ではない。電子の波とは、電子がさまざまな場所に同時に存在しているという状況を数式で表したものだと言える。以下、電子の波について説明するが、初めて聞く人には抽象的で分かりにくいかもしれない。しかし、とりあえずは「そういうものか」と考え、読み進めてもらいたい。
さて、前回までに繰り返し説明してきたが、一つの電子はさまざまな位置に同時に存在することができる。図1のx軸上に描いた多数の球は、一つの電子がさまざまな位置に存在している状態が重ね合わさっていることを表している。
ただし、それぞれの位置の状態には”濃淡”がある。電子の発見確率はそれぞれの位置で異なっているのだ。その発見確率の濃淡を数式で表し、グラフにすると、図1のような波の形になるのである。

電子の波のグラフは、x軸から離れた場所ほど、電子の発見確率が高いことを表している。つまり波の山または谷の位置で、電子の発見確率が最大(より正確には極大)になるのである。なお、発見確率と関係するのは、y座標の絶対値、つまりx軸からの距離(変位と呼ぶ)であり、谷の位置でも発見確率が最大になることに注意してほしい。x軸と波のグラフの線が交わる場所は発見確率がゼロなので、ここで電子が発見されることはない。以上のような電子の波を量子力学では「波動関数」と呼んでいる。
ミクロな粒子は”モノ”でもあり、”コト”でもある!?
本来、粒子と波は全く異なる性質をもつ存在だ。例えば、粒子は1カ所のみに存在しているが、波は空間に広がって存在している。電子は、粒子と波という相反する2つの側面をもつ奇妙な存在なのである。
電子が波の性質をもつというのは、よくよく考えると非常に不思議なことである。電子はあらゆる物体(モノ)を細かく分けていくと現れてくるものだったはずだ。常識的に考えれば、モノはモノからできているはずなので、電子もモノのはずだ。しかし波は現象、つまり“コト”だ。モノを細かく分けて行ったら、そこからコトが出てきたことになる。これが量子力学の不思議さの核心部分だと言ってもいいだろう。
2重スリット実験
光は2重スリット実験によって、「波」であることが実証された
それでは2重スリット実験について説明しよう。2重スリット実験とは、1805年頃にイギリスの物理学者トマス・ヤング(1773〜1829)が「光は波(波動)である」ということを実証した実験である。当時、光の正体を巡っては2つの説があった。粒子説と波動説だ。粒子説の支持者として有名なのは、力学(物体の運動を支配する法則についての物理学)の基礎を築いた物理学者アイザック・ニュートン(1642〜1727)である。
2重スリット実験とは以下のようなものだ(図2aと図2b)。光源の先に壁があり、壁には細長い2本の隙間(スリット)が開いている。壁の向こうにはスクリーンがあり、ここに光源からやってきた光が当たる。

仮に光が粒子だとして2重スリット実験を考えてみよう。光の粒は直進するはずなので、スクリーンには、それぞれのスリットの先に2本の光の帯が出現するはずだ(図2a)。しかし実際に実験を行うと、異なる結果が現れた。スクリーンには明暗の縞模様ができたのだ(図2b)。実はこれは、光が波の性質をもっていることを意味している。
波が起こす特有の現象に「回折」と「干渉」がある。回折とは、障害物があってもその陰の部分にまで、波が広がって進んで行く現象のことだ。例えば、塀の向こう側の会話の声(音波)が聞こえるのは、音波が回折を起こし、塀の陰の部分にも届くからである。2重スリット実験では、スリットを通った光の波が回折を起こし、扇状に広がって進んで行く。
スリットが2つあると、壁の先で左右のスリットを通った2つの波(波Aと波B)が重なり合うことになる。波が重なり合うと、強め合ったり弱め合ったりする現象が起きる。これを「干渉」と呼ぶ。例えば、波Aの山と、波Bの山が重なった場所では、より高い山ができる(強め合う干渉)。また、波Aの山と、波Bの谷が重なった場所では、波が打ち消しあってなくなってしまう(弱め合う干渉)。
光の波の高さ(振幅)は、光の明るさに対応するので、スクリーン上の強め合う干渉を起こした場所は明るくなり、弱め合う干渉を起こした場所では暗くなる。その結果、スクリーンには、明暗の縞模様ができるのである。このような波の干渉によって生じる縞模様は「干渉縞」と呼ばれる。ヤングが行った光の2重スリット実験では、干渉縞が現れ、そのため「光は波である」ということが実証されたのである[3]。
[3]ただし現在では、光の粒である「光子」は電子と同じく、粒子と波の2重性をもつことが明らかになっている。光が粒子的な性質をもつことを明らかにしたのは、アルバート・アインシュタインで1905年のことである(光量子仮説の提唱)。なお、アインシュタインは相対性理論で有名だが、1921年のノーベル物理学賞は相対性理論に対する功績ではなく、光量子仮説の功績に対して贈られている。
「世界一美しい実験」と称された電子の2重スリット実験
1989年、日立製作所の外村彰氏[4](1942〜2012)らは、電子を使って2重スリット実験を行うことに成功し、光の場合と似た干渉縞が生じることを明らかにした。つまり、電子は波の性質もっていたのである。
電子の2重スリット実験の実際のシステムは、図2とは少し異なっているが、本質的には光の2重スリット実験と同様の実験だと考えてよい(詳しくは日立製作所のウェブサイトを参照)。電子源は、出力を極限まで弱くすることで、電子を1つずつ発射することができる。また、光での実験におけるスクリーンの代わりに、2重スリットの先には平面状の検出器が置かれており、電子が到達した場所はモニター上に白い点として記録されていく。
さて、電子を1つずつ発射していくと、白い点は1つずつ増えていく。電子が単純な粒子だとしたら、これを多数回繰り返せば、図2aと同じように、それぞれのスリットの先に当たる場所に、多数の白い点でできた帯が現れるはずだ。しかし驚くべきことに、実際に実験を行うと、光の2重スリット実験と同じような干渉縞が現れたのである。
モニターには1つずつ白い点が増えていくので、これだけ見ると電子は粒子(1カ所にだけ存在しているモノ)のように思える。しかし、多数の点が描き出した模様は、電子を粒子と考えた場合に予測される2つの帯ではなく干渉縞であり、これだけ見ると電子は波のように思える。
[4]外村氏は「アハラノフ‐ボーム効果(AB効果)」という現象を実証した業績でも有名で、生前はノーベル物理学賞の候補者としてよく名前が挙がっていた。
スリットの先では、2つの波が「重ね合わせ状態」になっている
以上の矛盾しているようにも思える2重スリット実験の結果を、物理学者たちはどう解釈しているのだろうか? 以下、量子力学の標準的な解釈に基づいて説明しよう。
まず、電子は検出器で観測される前は、波として振る舞うと考える。電子源から放出された電子の波は広がりながら進み、2つのスリットを両方とも通過する。各スリットを通過した波は回折を起こしてさらに広がりながら進んで行く。左のスリットを通った電子の波を「波A」、右のスリットを通った電子の波を「波B」と表すことにしよう。スリットの先で電子は、波Aと波Bの「重ね合わせ状態」になっていることになる(図2bと同じ状況)。波Aと波Bが広がりながら進むと、これらの2つの波は重なり合って干渉を起こす。
そして電子の波が検出器に到達すると、極めて不思議なことが起きる。広がって存在していたはずの電子の波が瞬時にして1カ所に縮まり(図3)、その結果、検出器の1カ所でのみ電子が検出されるのだ。これを「波の収縮」と呼ぶ。波の収縮の結果、画面上には1つの白い点が現れる。1カ所に集まった針のような波は、その1カ所で必ず発見されることを意味するので、これは粒子としての電子と同じものを表していることになる。
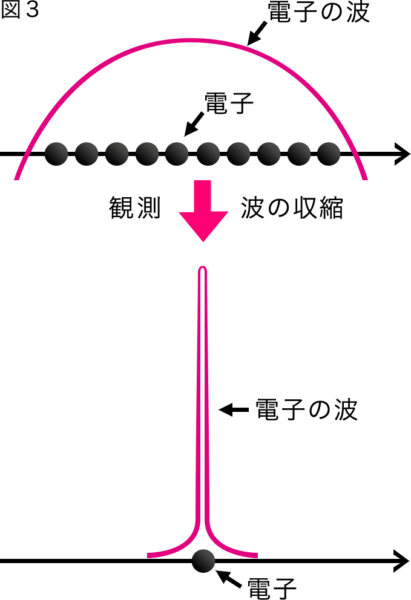
電子の波の変位(x軸からの距離)は前述したように、発見確率と対応している。そのため何度も何度も電子を発射すると、干渉を起こしてできた波の変位が大きい場所ほど、多くの電子が発見されることになる。逆に弱め合う干渉を起こして変位がゼロになった場所では、電子は発見されない。その結果、この実験を繰り返していくと、最終的に干渉縞が現れるのだ。
なお、外村氏らによる電子の2重スリット実験は、Physics World誌が2002年に行った読者アンケートで、「歴史上、最も美しい実験」に選ばれている。量子力学の不思議な性質が非常にはっきりとした形で表れた、素晴らしい実験だと言えるだろう。
以上の実験で重要なことは、スリットの先で電子の波Aと波Bが同時に存在していないと(重ね合わせ状態になっていないと)干渉は起きず、したがって干渉縞も現れない、ということだ。ある意味で、1つの電子がスリットAとスリットBを両方とも通過したと言えるわけだ。
どちらのスリットを通過したかを確認すると、干渉縞は現れない
しかし、1つの電子が2つのスリットを両方とも通過するなんてことが本当にあり得るのだろうか? 「本当は電子はどちらか一方のスリットを通過したが、観測者はそれを知らないだけ」なのではないだろうか?
それを確かめるために、スリットAのそばに、電子が通過したかどうかを知ることができる検出器を置くことを考えてみよう。そのような実験を行うと、不思議なことに、実験を繰り返しても干渉縞は現れず、図2aと同じように、スリットの先にそれぞれ明るい帯ができるだけとなる。スリットのところで電子を「観測」すると、波の収縮が起きて(重ね合わせ状態が崩れて)、電子が粒子のように振る舞うようになる。その結果、波の干渉は起きず、干渉縞が現れなくなるのだ[5]。
[5]干渉縞を現れないようにするには、検出器をスリットAとスリットBの両方に置く必要はない。どちらか一方に検出器を置くだけで十分である。スリットAのそばだけに検出器を置いた場合、検出器が反応せず、その後、モニターに白い点が現れれば、それは電子がスリットBを通過したことを意味し、事実上、スリットBの通過を観測したのと同じことになるからだ。これを「否定型測定」と呼ぶ。
このように、観測をどこで行うかによって、実験結果が変わってしまうというのが2重スリット実験の極めて不思議なところであり、量子力学の核心部分でもある。
2重スリット実験では、「電子がスリットAを通過した」という状態と、「電子がスリットBを通過した」という状態が重ね合わせ状態になっているが、ミクロな世界では、さまざまな状態が重ね合わせになりうる。量子コンピューターでは、量子ビットの重ね合わせ状態を使って計算を行うわけだが、量子ビットにはさまざまなタイプがある。例えば、①光の縦方向振動と横方向振動、②電子のスピン(自転に相当)の2つの向き、③イオンのエネルギーが高い状態と低い状態、④超伝導回路[6]の中の電子のペアのある・なし──などをそれぞれ0と1に対応させ、それらを重ね合わせ状態にして量子ビットとして使っているのである。
[6]超伝導とは、ある種の物質が極低温において電気抵抗(電流の流れにくさを表す値)がゼロになる現象のことである。超伝導状態では、電流を担う電子の間に何らかの引力が働いて、2つの電子がペア(クーパーペア)となって動いている。
「波と粒子の2重性」とは結局、何なのか?
電子は粒子でもなければ、波でもない
「波と粒子の2重性」について、「電子は粒子でもあり、波でもある」と説明されることがよくあるが、個人的にはこの表現は誤解を招くのではないかと考えている。マクロな世界の粒子と波は相反する性質をもち、本来両立できるものではないからだ。電子は粒子のような性質をもち、かつ、波のような性質ももつが、粒子や波とは”別の何か”なのである。「電子のようなミクロなモノも、私たちが知っているマクロな世界の常識に基づいて説明できるはず」と考えるのがそもそも間違いなのだ。私たちがこれまで知らなかった種類の何かがミクロの世界には存在する、ということを、量子力学は明らかにしたのである。
量子力学を難しいと感じるのは、私たちの思考が”実数的”だからかもしれない
さて、前述したように、電子の波の変位(x軸からの距離)が大きい場所ほど、電子の発見確率が高くなる。これを数式で表したものが波動関数だが、実は波動関数が取る値は、普通の数(実数)ではない。波動関数は一般に「複素数」の値をとるのだ。
複素数について復習しておこう。0以外の普通の数は、2乗すると必ず正の値になる。正の数を2乗すると、もちろん正になるが、負の数も2乗したら必ず正になる。例えば、-2の2乗は、(-2)×(-2)で4になり、これは正だ。しかし数学者たちは「2乗して-1になる数」というものを考え出した。それが虚数iである(正確には、iは「虚数単位」と呼ばれる)。式で表すと、i2=-1ということになる。aとbを実数としたとき、a+biで表される数が複素数だ。
虚数はよく「存在しない数」などと呼ばれる。しかし電子のようなミクロな粒子は、虚数(複素数)を使わないと、その振る舞いを正しく説明できないことが分かっている。複素数という”拡張された数”を使って電子の波を表すことで、初めて量子力学の不思議な現象を説明することが可能になるのだ。
量子力学、すなわち自然界の法則には、虚数の存在が不可欠なのである[7]。その意味では、虚数を「存在しない数」と呼ぶのは不適切だと言えるだろう。私たちの存在もミクロな視点から見れば、ある意味で虚数的(複素数的)なのだから。
[7]虚数(複素数)は、量子力学以外の物理学でも使われることがある。例えば、電気回路を流れる電流の値を計算する際などに使われる。ただし、量子力学以外の分野では、虚数は「計算を楽にするための道具」として使われているのであって、虚数なしで計算することもできるのが普通である。しかし量子力学は虚数抜きでは成立しない。量子力学で最も重要な基礎方程式である「シュレーディンガー方程式」にも、虚数が含まれているのだ。
電子の波(波動関数)は観測前は複素数的に振る舞う。しかし観測すると、その実数的な姿、すなわち粒子としての姿を現わす。私たちが電子の波について不思議に感じ、量子力学についてなかなか実感をもって理解できないのは、私たちの思考が実数的だからなのかもしれない。
第4回につづく(9/1掲載予定)





